Magazine PROF n°40

Libres propros 

Mieux articuler arithmétique et algèbre entre primaire et secondaire

Article publié le 07 / 12 / 2018.
Article paru en ligne uniquement.

Cette rubrique permet à un expert de faire part d’un message qu’il juge important dans le contexte actuel. Isabelle Demonty invite à penser la transition au cœur même de la discipline enseignée. Illustration avec l’articulation entre arithmétique et algèbre lors du passage du primaire au secondaire.

Les transitions dans l’enseignement sont des moments clés dans la progression des élèves. Lors de ces transitions, certains contenus sont semblables. Pourtant les élèves perçoivent peu la continuité des apprentissages dans ces notions, considérant que les manières de les aborder sont très différentes aux deux niveaux d’enseignement considérés.

Ce problème se pose particulièrement lors de la transition entre le primaire et le secondaire où l’on assiste à un passage de l’arithmétique vers l’algèbre. Que peut-on faire dès l’école primaire pour aider les élèves à réinvestir leurs acquis arithmétiques lorsque l’algèbre sera introduite ? Comment à l’école secondaire, faire davantage de connections avec ce qui a été appris avant ?

Ces questions sont à l’origine de recherches collaboratives réunissant des chercheurs, des conseillers pédagogiques, des instituteurs et des régents en mathématiques. Les travaux ont approché ces questions au travers d’activités : l’idée était de mettre au point des situations permettant aux élèves de développer des manières de raisonner qui prennent racine en arithmétique et qui sont essentielles pour comprendre l’algèbre.

Au travers de la présentation des deux éléments clés permettant de favoriser davantage de continuités entre l’arithmétique et l’algèbre, cet article vise à montrer l’intérêt de penser la question de la transition en relation directe avec les apprentissages essentiels à réaliser aux deux niveaux d’enseignement concernés.

Un travail sur l’égalité et les propriétés des opérations

L’apprentissage des techniques de calculs mentaux est un des piliers de l’arithmétique. La plupart des élèves arrivent en secondaire avec des procédures pour réaliser ces calculs. Pourtant, même ceux qui les utilisent correctement éprouvent des difficultés à faire la transition vers les calculs algébriques.

Ces difficultés sont souvent liées à un manque de compréhension des propriétés des opérations et de l’égalité : les élèves comprennent parfois ces propriétés dans le domaine arithmétique, mais n’y ont plus accès dans le nouveau contexte qu’est pour eux l’algèbre. D’autres élèves ont mémorisé ces procédures mais ne comprennent pas pourquoi elles fonctionnent ni en quoi elles sont basées sur les propriétés des opérations.

Enseigner ces techniques dès l’école primaire, avec en point de mire, un travail sur les propriétés des opérations, permet de faire apparaitre les continuités entre l’arithmétique et l’algèbre. Réinvestir ces propriétés lors des premiers apprentissages algébriques contribue à prolonger la réflexion ainsi amorcée au primaire.

La situation suivante concrétise cette idée.

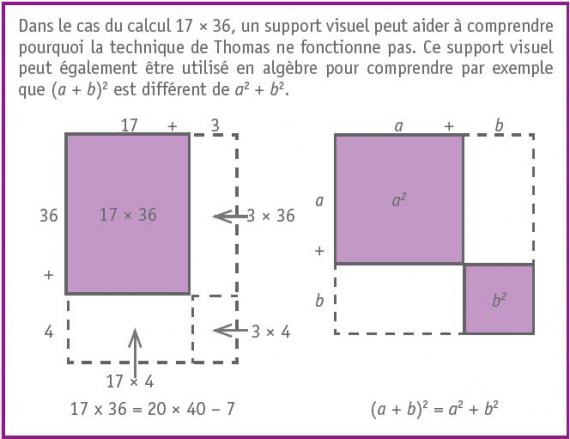
La méthode de Thomas illustre une erreur qui consiste à appliquer une technique qui fonctionne pour une opération (ici l’addition) à une autre opération (ici la multiplication). En effet, si l’opération à effectuer est 17 + 36, la technique de Thomas fonctionne : 17 + 36 = 20 + 40 – 3 - 4 = 53.

Cette erreur, on la retrouve sous d’autres formes en algèbre : par exemple, les élèves considèrent à tort que (a + b)² = a² + b², or la démarche aurait été correcte si, dans la parenthèse, l’opération avait été une multiplication et non une addition…

En amenant les élèves à comprendre pourquoi la règle de Thomas ne fonctionne pas, l’enseignante les fait réfléchir sur une propriété de la multiplication (la distributivité) dans le but de comprendre le rôle du 3 et du 4 que Thomas a additionnés. Et ces propriétés des opérations sont également à la base des calculs algébriques. En travaillant explicitement ces propriétés, à l’aide par exemple de supports visuels, on donne l’occasion aux élèves de percevoir la continuité entre l’arithmétique et l’algèbre.

Développer une pensée impliquant des quantités indéterminées

On peut faire un pas de plus dans la recherche d’articulations en cherchant des formes de raisonnements particulièrement sollicitées en algèbre et qui peuvent déjà être amorcées en arithmétique. Historiquement, l’algèbre est apparue lorsqu’on a commencé à réaliser des opérations impliquant des quantités indéterminées : cette capacité est donc une caractéristique essentielle de l’algèbre, qu’il est possible d’exploiter dès l’école primaire.

Les activités de généralisation constituent un environnement riche pour développer ce type de raisonnement. Voici un exemple d’une telle activité :

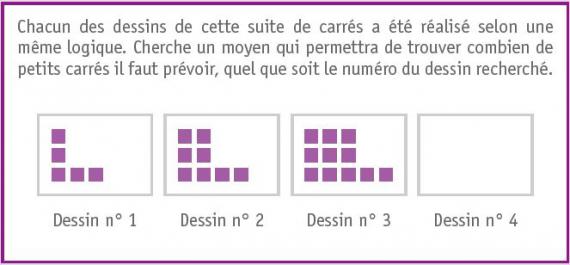
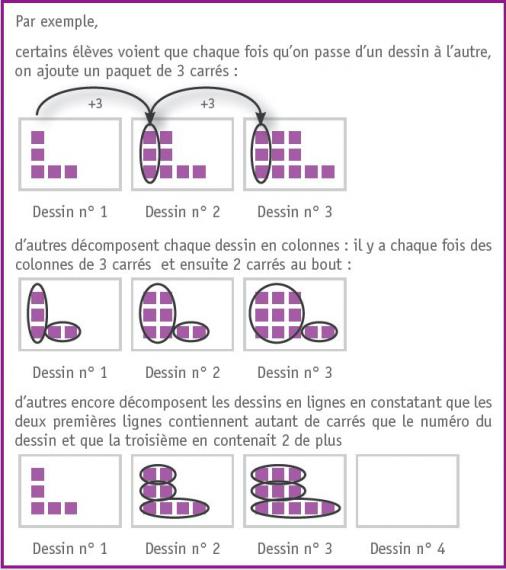
L’intérêt de cette activité est qu’il y a de nombreuses logiques de construction et que les élèves, qu’ils aient onze, douze ou quatorze ans, ont beaucoup d’idées. Ces dernières pourront être exploitées en primaire au travers de calculs sur des nombres et se prolonger, en secondaire, au travers de calculs sur des lettres.

Changer le regard porté
sur les activités arithmétiques et algébriques

Articuler l’arithmétique et l’algèbre n’implique pas d’enseigner de manière précoce l’algèbre, ni même de changer fondamentalement les activités du primaire ou du secondaire. C’est plutôt le regard porté sur celles-ci qui doit évoluer. En amenant les élèves à analyser des calculs, non pas en comparant leur réponse, mais plutôt les opérations qu’ils impliquent ; en développant des raisonnements impliquant des quantités indéterminées ; les instituteurs peuvent susciter une meilleure compréhension de l’arithmétique tout en installant les bases du raisonnement algébrique.

De la même façon, les enseignants du secondaire ont un rôle à jouer pour que les premiers apprentissages algébriques s’insèrent plus directement dans les stratégies arithmétiques des élèves, de manière à ce que l’algèbre ne constitue plus pour les élèves cette matière isolée, sans lien avec les acquis du primaire.

L’ensemble de ces considérations montre, nous l’espérons, l’importance d’envisager la question de la transition au cœur même des disciplines enseignées.

Isabelle DEMONTY